力学的エネルギー保存の法則（３） |
   |
力学的エネルギー保存の法則（３） |
|
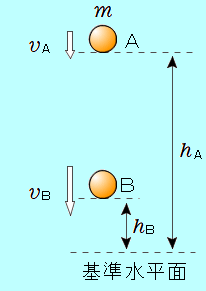 力学的エネルギー保存の法則図のように、質量  〔ｋｇ〕の小球が自由落下をしているとき、基準水平面から高さ Ａ〔ｍ〕の点Ａを速さ Ａ〔ｍ/ｓ〕で、高さＢ〔ｍ〕の点Ｂを速さＢ〔ｍ/ｓ〕で通過したとします。 点Ａと点Ｂの運動エネルギーの関係を、エネルギーの原理（運動エネルギーの変化＝その間にされた仕事）から求めます。 運動エネルギーの変化は、  （「〜の変化」は「後 − 前」） この間に、重力がした仕事は、  ＝  ＝ ×(Ａ−Ｂ)よって、エネルギーの原理は、  Ａ点に関する項とＢ点に関する項を左辺と右辺に分けて整理すると、  となります。 左辺、右辺ともに、第１項は各点での運動エネルギー、第２項は各点での重力による位置エネルギーを表します。 つまり、各点での運動エネルギーと位置エネルギーの和は変わらないということです。 これは、重力による位置エネルギーだけでなく、弾性力による位置エネルギーについても同様のことが言えます。 運動エネルギーと位置エネルギーの和を、「力学的エネルギー」といいます。 物体が、重力や弾性力だけから仕事をされ、他に仕事をされることも仕事をすることもなく運動する場合、その力学的エネルギーは一定に保たれます。これを、力学的エネルギー保存の法則といいます。
力学的エネルギーを と表し、今までどおり運動エネルギーを 、位置エネルギーを と表すと、力学的エネルギー保存の法則は、＝＋＝ 一定 …教科書ｐ105 (79)式と表すことができます。 |
|||
| → 力学的エネルギー保存の基本例題 へ |
|||
| |
|||
| |
|||
