 糸で連結された物体の運動の場合(p74) 糸で連結された物体の運動の場合(p74)
糸で連結された2物体の運動についても、「2つの物体が力を及ぼし合っている場合の運動」ですので、前のページと同じ手順で扱います。
 例として、問題集p44問題87で考えます。 例として、問題集p44問題87で考えます。
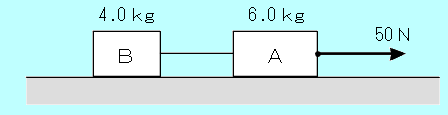
問題87 なめらかな水平面上に、質量 6.0kgの物体Aと質量 4.0kgの物体Bがあり、糸で結ばれている。
Aを右向きに50Nの力で引く場合、A,Bの加速度の大きさと糸の張力の大きさを求めよ。
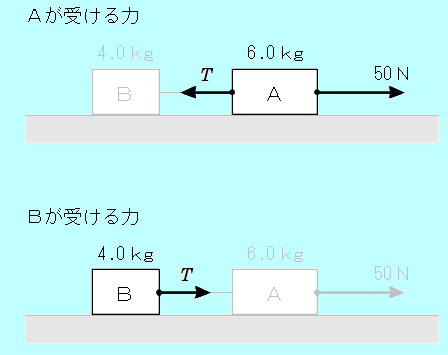
 物体ごとに、その物体が受けている力を描く 物体ごとに、その物体が受けている力を描く
求める加速度の大きさを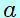 〔m/s2〕、糸の張力の大きさを 〔m/s2〕、糸の張力の大きさを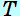 〔N〕とします。 〔N〕とします。
・なお、軽い糸の場合、張力はどこでも同じ大きさになります。(このページの下の方に解説があります)
・重力と垂直抗力はつり合っているので省略しました。
 物体ごとに運動方程式 物体ごとに運動方程式 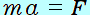 をたてる をたてる
図の右向きを正の向きとします。
物体Aについて 6.0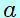 = 50− = 50−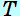 … … 式 式
物体Bについて 4.0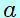 = =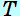 … …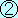 式 式
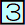 運動方程式を連立させて、問題を解く 運動方程式を連立させて、問題を解く
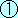 式+ 式+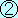 式より 式より
10.0×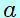 = 50 = 50
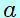 = 5.0 = 5.0
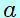 = 5.0を = 5.0を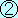 式に代入 式に代入
4.0×5.0 =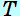
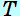 = 20 = 20
よって
A,Bの加速度の大きさ 5.0 m/s2
糸の張力の大きさ 20 N
 軽い糸の場合、糸の張力の大きさはどこでも等しくなります 軽い糸の場合、糸の張力の大きさはどこでも等しくなります
図1 物体A,Bが、糸から受ける力
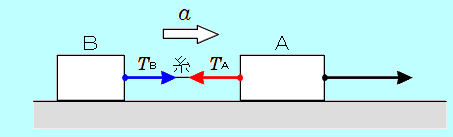
図1の状況で、物体Aが糸から受ける張力の大きさを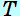 A、物体Bが糸から受ける張力の大きさを A、物体Bが糸から受ける張力の大きさを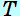 Bとおきます。全体が、加速度の大きさ Bとおきます。全体が、加速度の大きさ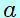 で図の右向きに運動しているとします。 で図の右向きに運動しているとします。
図2 糸が、物体A,Bから受ける力
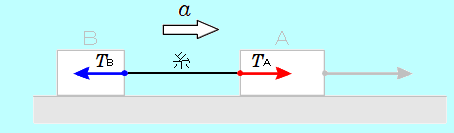
作用・反作用の法則から、図2のように、糸は、大きさ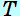 Aの力を物体Aから、大きさ Aの力を物体Aから、大きさ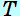 Bの力を物体Bから受けます。 Bの力を物体Bから受けます。
図2の右向きを正の向きとして、糸の運動方程式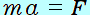 を書きます。 を書きます。
軽い糸の場合、質量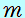 =0と考えます。(「軽い」という表現は物理では「質量が無視できる」という意味です) =0と考えます。(「軽い」という表現は物理では「質量が無視できる」という意味です)
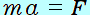 より より
0×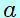 = =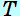 A− A−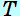 B B
よって、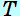 A= A=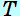 B となり、「軽い糸の場合、糸の張力の大きさはどこでも等しい」ことになるのです。 B となり、「軽い糸の場合、糸の張力の大きさはどこでも等しい」ことになるのです。
|
|

