力のつりあい（３） |
   |
力のつりあい（３） |
|
 教科書ｐ59 類題６一端を壁に固定した長さ 0.50ｍの糸Ａに、重さ12Ｎの物体をつるし、図のように、別の糸Ｂで引くと、物体は壁から 0.30ｍはなれて静止した。糸Ａ、Ｂの張力の大きさは、それぞれ何Ｎか。 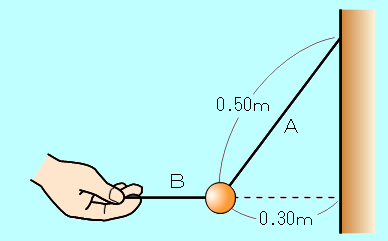 ＜解答の前に＞辺の比が、３：４：５の三角形は、三平方の定理に当てはまりますので、直角三角形になることがわかります。 ３２＋４２＝５２ 下図の、斜線を付けた直角三角形は、辺の長さが 0.30ｍ、0.50ｍなので、辺の比が３：４：５の直角三角形となります。 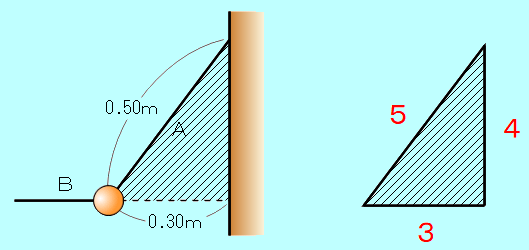 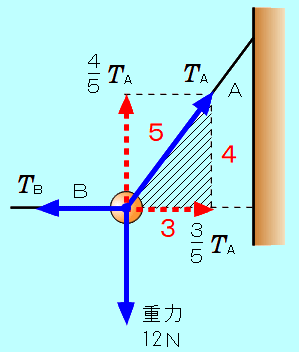解法１＜それぞれの力の水平成分、鉛直成分のつりあいで考える＞ 図のように、糸Ａ、Ｂの張力の大きさを、それぞれ  Ａ〔Ｎ〕、Ｂ〔Ｎ〕とします。糸Ａの張力の水平成分、鉛直成分の大きさを、三角形の辺の比から求め、水平方向と鉛直方向のそれぞれの力のつりあいの式を書きます。 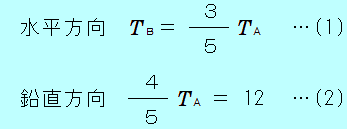 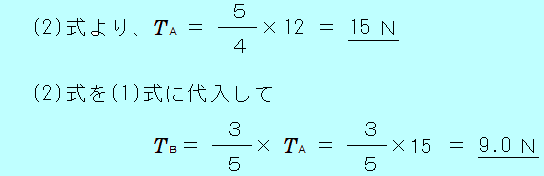 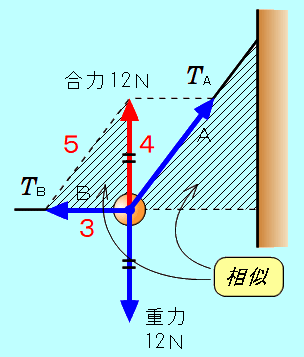解法２＜平行四辺形の法則で合成して考える＞ 図のように、糸Ａ、Ｂの張力の大きさを、それぞれ Ａ〔Ｎ〕、Ｂ〔Ｎ〕とします。糸Ａ、Ｂの合力が、物体にはたらく重力（12Ｎ）とつりあっていると考えると、合力の大きさも 12Ｎ となります。 図の、斜線を付けた直角三角形の辺の比が、３：４：５となるので、  |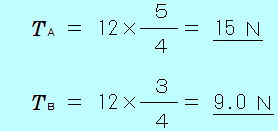
||
| → 作用・反作用の法則 へ |
||
| |
||
| |
||