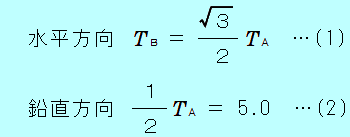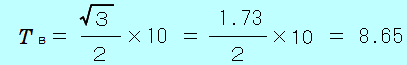3力のつりあい(教科書p58〜59) 3力のつりあい(教科書p58〜59)
例題6(教科書p59)より
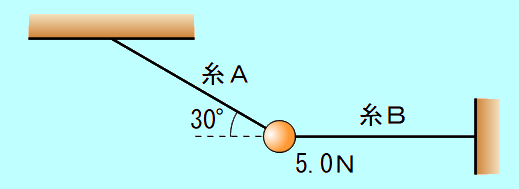
図のように、重さ 5.0Nの物体が、2本の糸A、Bにつながれて静止している。糸Aは水平方向から 30°上向きに、糸Bは水平に張られている。このとき、糸A、Bの張力の大きさは何Nか。
 解法1<水平成分、鉛直成分の力のつりあいで考える> 解法1<水平成分、鉛直成分の力のつりあいで考える>
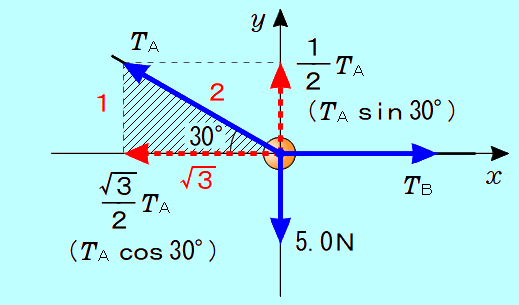
図のように、糸A、Bの張力の大きさを、それぞれ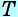 A〔N〕、 A〔N〕、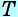 B〔N〕とします。 B〔N〕とします。
糸Aが、斜めなので、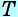 Aの水平成分、鉛直成分の大きさを、三角形の辺の比(1:2: Aの水平成分、鉛直成分の大きさを、三角形の辺の比(1:2: )から求め、水平方向と鉛直方向のそれぞれの力のつりあいの式を書くと、次のようになります。 )から求め、水平方向と鉛直方向のそれぞれの力のつりあいの式を書くと、次のようになります。
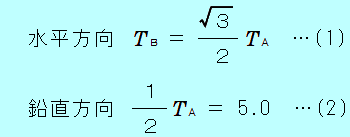
教科書の解法では、三角比(sin30°、cos30°)を用い、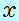 軸、 軸、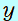 軸の正負の符号を考慮して、次のように表しています。 軸の正負の符号を考慮して、次のように表しています。
水平方向 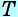 B− B−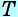 A cos30°=0 …教科書(1) A cos30°=0 …教科書(1)
鉛直方向 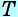 A sin30°− 5.0 =0 …教科書(2) A sin30°− 5.0 =0 …教科書(2)
上の(1)、(2)と教科書(1)、教科書(2)のどちらの表し方でもかまいません。(同じ式となります)
|
(2)式より
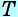 A= 2×5.0= 10N A= 2×5.0= 10N
(1)式に代入して
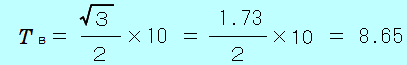
よって、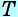 B= 8.7N B= 8.7N
 解法2<平行四辺形の法則で合成して考える> 解法2<平行四辺形の法則で合成して考える>
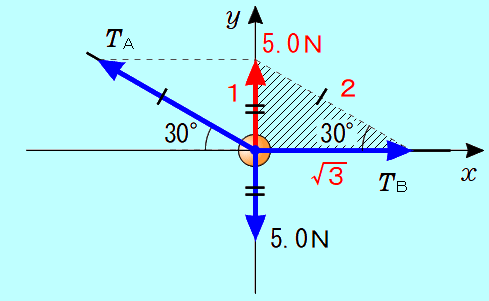
図のように、糸A、Bの張力の合力が、物体にはたらく重力の大きさ(重さ)5.0Nとつりあっていると考えると、糸A、Bの張力の合力の大きさは、5.0Nとなります。
図の、斜線を付けた三角形の辺の比を参考に、糸A、Bの張力の大きさを求めることができます。
糸A 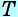 A= 5.0×2= 10N A= 5.0×2= 10N
糸B 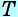 B= 5.0× B= 5.0× = 5.0×1.73 = 8.65 よって、 = 5.0×1.73 = 8.65 よって、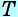 B= 8.7N B= 8.7N
|