自由落下と鉛直投げおろし(5) |
|
| 教科書「問」の解答 |
||
ビルの屋上から小球を静かに落としたところ、3.0秒後に地面に落下した。地面からのビルの高さは何mか。また、小球が地面に達する直前の速さは何m/sか。ただし、重力加速度の大きさを 9.8m/s2とする。 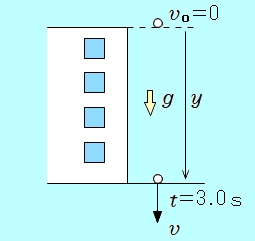 ビルの高さについて 3.0秒の落下距離がビルの高さになるので、等加速度2本目の式 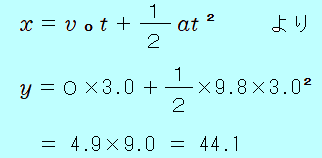 2ケタ×2ケタの計算で有効数字は2ケタだから、ビルの高さは 44m 地面に達する直前の速さについて 3.0秒後の速さなので、等加速度1本目の式 有効数字2ケタだから、求める速さは 29m/s |
||
海面からの高さが 4.9mの橋の上から、小球を自由落下させた。小球が海面に達する直前の速さは何m/sか。また、海面に達するまでの時間は何秒か。ただし、重力加速度の大きさを 9.8m/s2とする。 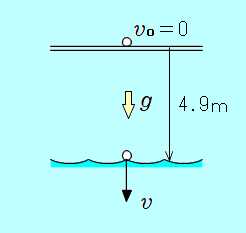 海面に達する直前の速さについて 時間がわからず、落下距離 4.9mがわかっているので、等加速度3本目の式 ( よって、海面に達する直前の速さは 9.8m/s 海面に達するまでの時間について 橋から海面までの距離 4.9mが与えられているので、等加速度2本目の式 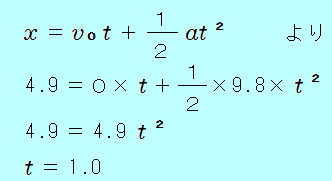 答え 1.0 秒 <別解> 初めに、海面に達する直前の速さ 9.8m/sを求めたので、等加速度1本目の式 9.8 =0+9.8 ただし、初めの「海面に達する直前の速さ」を間違えていると、こちらも不正解となってしまいます。 |
||
水面からの高さが 14.7mの橋の上から、ある初速度で小球を鉛直下向きに投げたところ、1.0秒後に水面に達した。小球の初速度の大きさと、水面に達する直前の速さは何m/sか。ただし、重力加速度の大きさを 9.8m/s2とする。 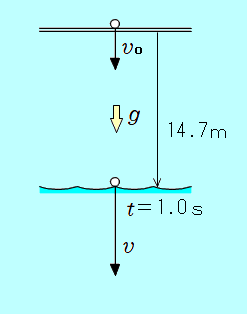 初速度の大きさについて 1.0秒で 14.7m落下したのだから、等加速度2本目の式 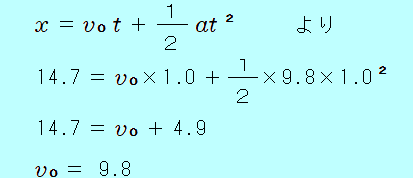 答え 初速度は 9.8m/s 水面に達する直前の速さについて 水面に達するまでの時間が示されているので、等加速度1本目の式 = 19.6 答え 19.6m/s |
||
ビルの屋上から小球Aを自由落下させ、その 1.0秒後に、小球Bを速さ 19.6m/sで鉛直下向きに投げおろした。Bを投げてから、何秒後にBがAに追いつくか。また、そのときのBの速さは何m/sか。ただし、重力加速度の大きさを 9.8m/s2とする。 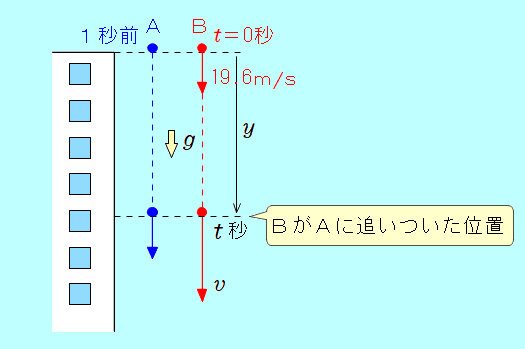 Bを投げおろしてから、BがAに追いつくまでの時間について Bを投げおろした時刻を 時刻 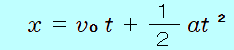 を用いて表しますが、 を用いて表しますが、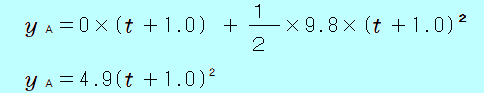 時刻 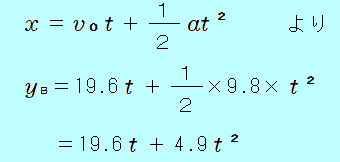 「BがAに追いつく」とは、AとBが同じ位置(落下距離が等しい)となったときなので 4.9( 両辺を 4.9で割って 1.0 = 2 答え BがAに追いつくのは、Bを投げてから 0.50秒後 そのときのBの速さについて 等加速度1本目の式 = 19.6 + 4.9 = 24.5 答え 24.5m/s できましたか? |
||
 |
||
| → 初めのページへ |
||
| |
||