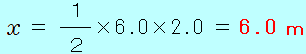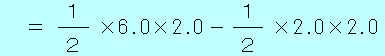問題練習 問題練習
「問題集 p10 問題21」(改題)で練習します
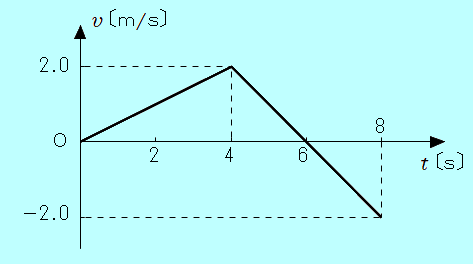
図は、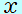 軸上を運動する物体の速度 軸上を運動する物体の速度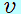 〔m/s〕と時刻 〔m/s〕と時刻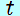 〔s〕との関係を表している。物体は、 〔s〕との関係を表している。物体は、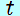 =0 のときに原点を出発したものとして、次の各問に答えよ。 =0 のときに原点を出発したものとして、次の各問に答えよ。
(1) 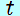 =2.0sにおける物体の加速度を求めよ。 =2.0sにおける物体の加速度を求めよ。
(2) 物体が出発点から正の向きに最も遠ざかる時刻とそのときの位置を求めよ。
(3) 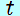 =8.0sにおける物体の位置を求めよ。 =8.0sにおける物体の位置を求めよ。
 <解答> <解答>
(1) 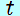 =0〜4.0sでは、4.0秒間で速度が0m/sから2.0m/sに変化しているので、この間の加速度は、加速度の式を用いると、 =0〜4.0sでは、4.0秒間で速度が0m/sから2.0m/sに変化しているので、この間の加速度は、加速度の式を用いると、

答え 0.50m/s2
(補足)
同じことですが、「 グラフの傾き」から加速度を求めてもいいです。 グラフの傾き」から加速度を求めてもいいです。
グラフの0〜4.0sの区間で傾きを求めるとよいです。
計算は、上と同じになります。
(2) 物体の運動は、次のようになります。
・速度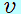 が正の値をとる0〜6.0sの区間は、物体は が正の値をとる0〜6.0sの区間は、物体は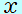 軸正の向きに運動する 軸正の向きに運動する
・時刻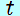 =6.0sで =6.0sで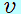 =0となるので、一瞬停止する =0となるので、一瞬停止する
・速度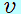 が負の値をとる6.0〜8.0sの区間は、物体は が負の値をとる6.0〜8.0sの区間は、物体は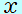 軸負の向きに運動する 軸負の向きに運動する
運動の状況は次の図のようになります。(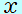 の値は、下の(2)、(3)が解けたものとして表示してあります。) の値は、下の(2)、(3)が解けたものとして表示してあります。)
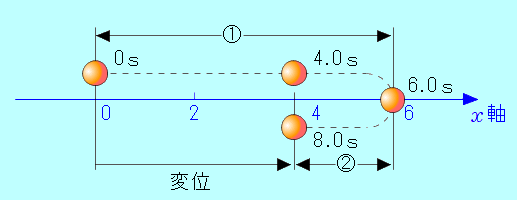
従って、物体が出発点から正の向きに最も遠ざかる時刻は、6.0秒 となります。
また、下の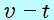 グラフの0〜6.0sまでの赤い三角形 グラフの0〜6.0sまでの赤い三角形 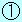 の面積が、出発点(原点)から正の向きに最も遠ざかる点までの距離を表します。 の面積が、出発点(原点)から正の向きに最も遠ざかる点までの距離を表します。
よって、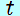 =6.0sの物体の変位 =6.0sの物体の変位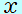 〔m〕は、 〔m〕は、
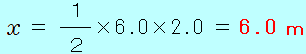
(3)
・上のグラフの時刻0〜6.0sまでの赤い三角形  の面積が、出発点(原点)から正の向きに最も遠ざかる点までの距離です。 の面積が、出発点(原点)から正の向きに最も遠ざかる点までの距離です。
・上のグラフの時刻6.0〜8.0sまでの青い三角形  の面積が、最も遠ざかる点から原点に向かって戻る距離を表します。 の面積が、最も遠ざかる点から原点に向かって戻る距離を表します。
・従って、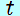 =8.0sにおける物体の位置 =8.0sにおける物体の位置 〔m〕は、( 〔m〕は、( の面積)−( の面積)−(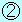 の面積)で求めることができます。 の面積)で求めることができます。
 =( =( の面積)−( の面積)−( の面積) の面積)
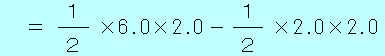
= 6.0−2.0 =4.0
答え 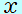 =4.0m =4.0m
|