[利用例2]p30「負の加速度の運動」
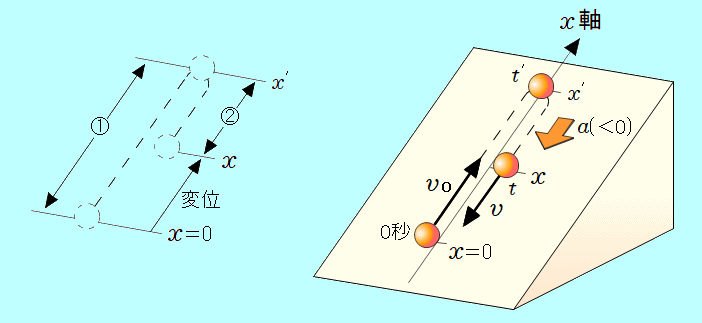
 図のように、斜面に沿って上向きに初速度 図のように、斜面に沿って上向きに初速度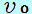 で小球を打ち出した時の運動を考えます。 で小球を打ち出した時の運動を考えます。
・打ち出した点を原点とし、斜面に沿って上向きを正の向きとする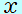 軸をとります。 軸をとります。
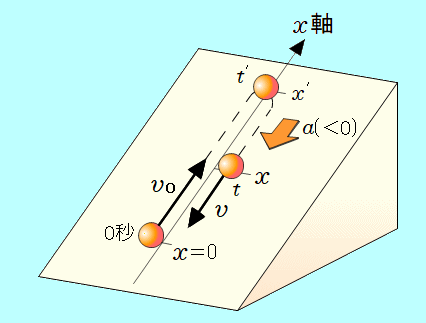
・小球は徐々に減速し、やがて速度が 0 となり、直ちに下向きに加速していきます。
加速度は負の向き(斜面に沿って下向き)です。
 この運動の この運動の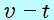 グラフを描きます。 グラフを描きます。
・小球の速度は、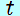 =0 のとき正の向きに初速度 =0 のとき正の向きに初速度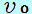
・小球は徐々に減速し、やがて時刻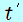 のとき のとき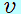 =0 となる =0 となる
・そのままの(負の)加速度で、小球の下向きの速さが大きくなっていく
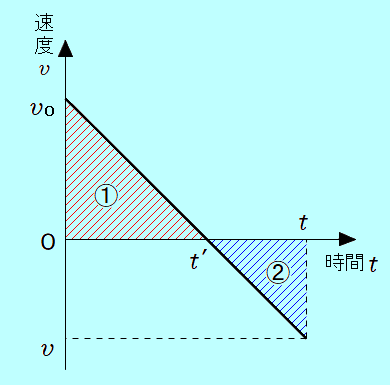
このとき、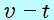 グラフは「面積が移動距離を表す」のだから、 グラフは「面積が移動距離を表す」のだから、
・ グラフの時刻 0 から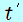 までの赤い三角形 までの赤い三角形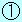 の面積が、打ち出した点から最高点までの移動距離(= の面積が、打ち出した点から最高点までの移動距離(=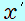 )を表します。 )を表します。
・ グラフの時刻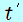 から から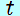 までの青い三角形 までの青い三角形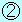 の面積が、図の、最高点から位置 の面積が、図の、最高点から位置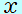 までの移動距離 までの移動距離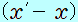 を表します。 を表します。
・ 打ち出してから時刻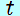 までに小球が移動した距離は、 までに小球が移動した距離は、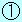 の面積+ の面積+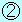 の面積となります。 の面積となります。
・ 打ち出してから時刻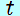 までの小球の変位(図の までの小球の変位(図の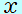 )は、 )は、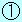 の面積− の面積−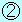 の面積となります。 の面積となります。
 このときの このときの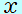 − −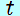 グラフは、「等加速度直線運動の グラフは、「等加速度直線運動の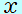 − −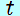 グラフは放物線のかたち」であることから、次のようになります。 グラフは放物線のかたち」であることから、次のようになります。
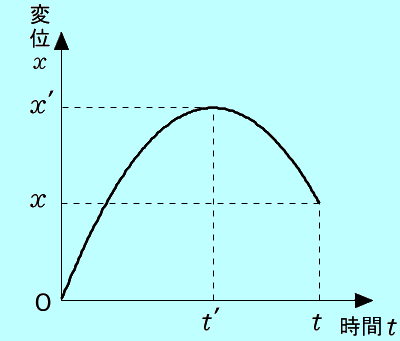
(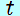 2 の係数が負(加速度 2 の係数が負(加速度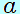 <0)ですから、グラフは上に <0)ですから、グラフは上に の放物線のグラフとなります) の放物線のグラフとなります)
|



