等加速度直線運動の３本の式（３） |
   |
等加速度直線運動の３本の式（３） |
|
| （２）時間と変位の式 「時刻  のと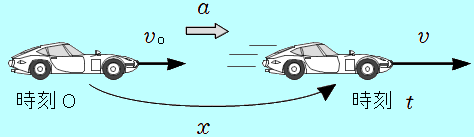き、変位はどれ程か（どの位置か）？」とか、「変位が になる時刻は？」とかを表す式です。＜状況＞  | ||
まず、上の＜状況＞の  グラフをえがきます。・時刻０のとき、速度は  ・時刻 のとき、速度は ・一定の割合で速度が増えていく（等加速度） これらのことから、 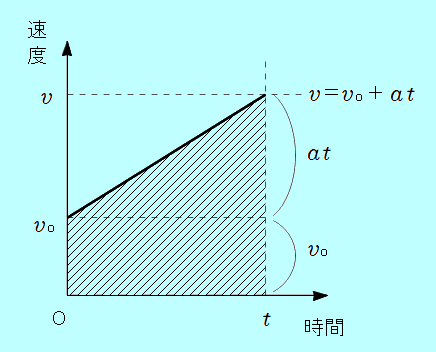グラフは次のようになります。 さて、図の斜線をつけた台形の部分は何でしょう。 以前「 グラフの面積が移動距離を表す」ことを学びました。（「02 等速直線運動のグラフ」のところ）よって、上の グラフの斜線部分の面積がを表すことになります。 | ||
グラフの高さ（）について、等加速度の１本目の式（１）より、 ですから、グラフの右側のように、と とを分けて考えることができます。斜線部分を下の長方形と上の三角形に分けて考えて、 ＝（台形の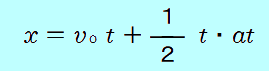面積）＝（長方形の面積）＋（三角形の面積）従って  少し整理して 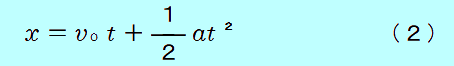 これが、大事な、等加速度２本目の式です。 「エックス イコール ブイゼロティー プラス にぶんのいち エーティーじじょう」と、風呂に入ったときにでも50回繰り返して覚えましょう。 | ||
| →
等加速度３本目の式へ |
||
| | ||
| | ||