波の表し方と波の要素（５）

 　ホームページへ　　
正弦波（教科書ｐ141）

波源が単振動する場合、下の図のような曲線の波ができます。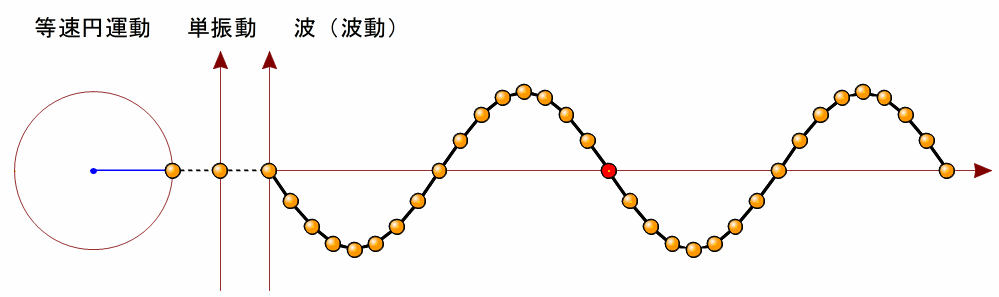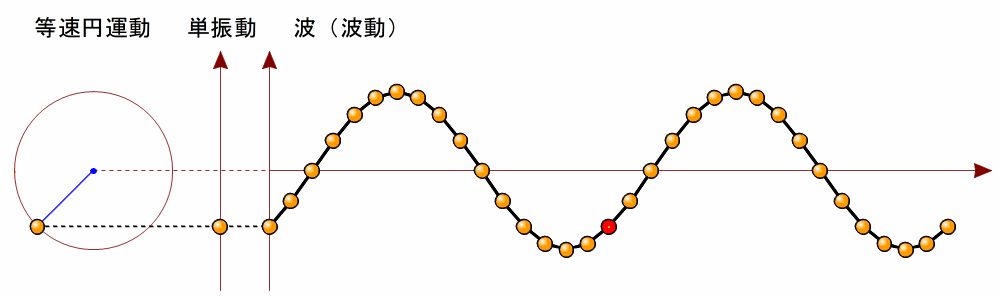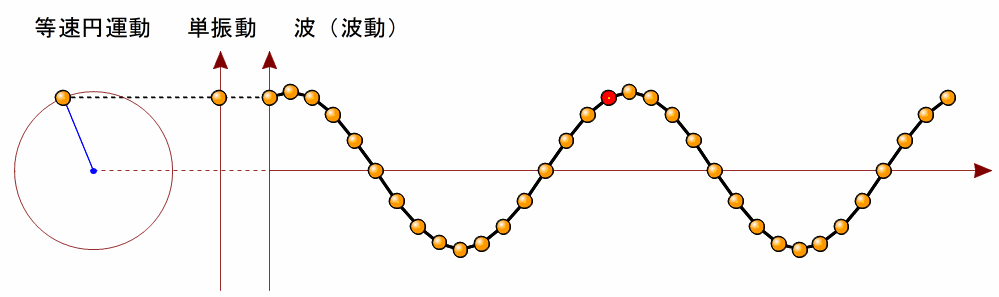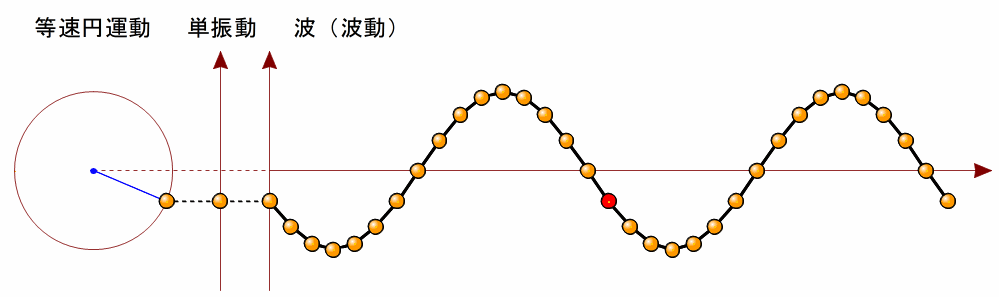



このような曲線を正弦曲線（＝ｓｉｎ で表される曲線）といいます。
波形が正弦曲線となる波を、正弦波といいます。


正弦波と波の要素（教科書ｐ142）

図のような正弦波について、波形の最も高いところを山、最も低いところを谷といいます。

また、正弦波は同じ波形の繰り返しとなっていますが、繰り返しの最小単位を波長といいます。
山から隣の山までの間隔でも良いし、谷から隣の谷までの間隔でもいいです。図のＡ点からＢ点の距離も波長です。

また、振動の中心からの山の高さまたは谷の深さを波の振幅といいます。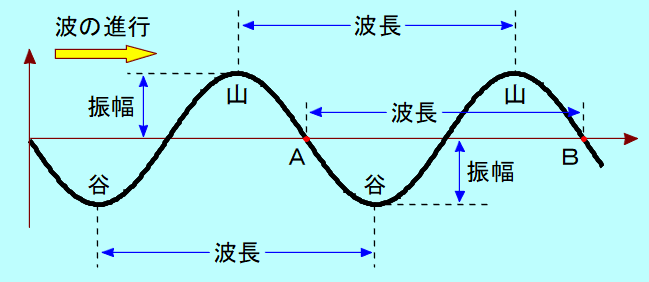
波の速さの式

３ページ前（波の表し方と波の要素（２））の波の発生のアニメーションをイメージしてください。
波源が振動し始めて、１回（１周期）振動すると、１個の波（１波長分の波）が発生します。波長を（ラムダ）とおきます。
波源が２回（２周期）振動すると、２個の波（２波長分の波）が発生して、波の先頭は２（２波長分）だけ先に進んでいます。
波源の振動数を（１秒間に回振動）とすると、１秒間に個の波が発生して、進行方向に進んでいます。

この１秒間に波が進んだ距離は、波長の倍になります。１秒間に、波は× だけ進んだことになります。
よって、波の速さをと置くと、
＜重要＞
　＝　　教科書ｐ142（2）式　




問題２（教科書ｐ142 問３）
周期 0.50秒、波長 2.0ｍの正弦波が伝わる速さは何ｍ/ｓか。


問題３（教科書ｐ141 ＴＲＹ 波形を描こう（改））

図のように、水平に張ったロープの左端を、図に示した矢印のように振動させるとき、ロープに生じる波形の概形を描け。
ただし、ロープに生じる波は、正弦波になるものとする。

(1)



(2)



(3)



(4)
 　
　→ 答え合わせ へ　
   
　ホームページへ