仕事の原理・仕事率（１） |
   |
 教科書ｐ92〜93 |
|
仕事の原理・仕事率（１） |
|
| 教科書ｐ92〜93 |
|
| 仕事の原理（教科書ｐ92） できるだけ楽に仕事をすることについて考えてみます。 図のように、Ａくん、Ｂくんが質量 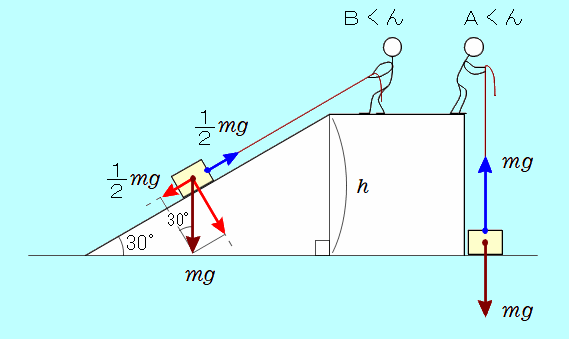 〔ｋｇ〕の荷物を高さ 〔ｍ〕だけ持ち上げる仕事を考えます。 Ａくんのする仕事Ａくんは、荷物をまっすぐ上に引き上げます。 Ａくんが荷物を引き上げるのに最低限必要な力は、荷物にはたらく重力と等しい、  〔Ｎ〕です。
さて、Ａくんは、 〔Ｎ〕の力で高さ〔ｍ〕だけ荷物を引き上げるので、Ａくんのする仕事は、 ＝  ＝ 〔Ｊ〕となります。 Ｂくんのする仕事Ｂくんは、「真上に引き上げるより、斜面を使えば楽に引き上げることができるよ。」ということで、30°のなめらかな斜面を利用して荷物を引き上げます。 荷物にはたらく重力の、斜面に平行な分力の大きさは、  ですから、Ｂくんが斜面を利用して荷物を引き上げるのに最低限必要な力は、荷物にはたらく重力の、斜面に平行な分力の大きさと等しい、 となり、Ａくんの半分の大きさの力で荷物を引き上げることができます。 ただし、Ｂくんが斜面上を荷物を引き上げる距離は、30°の斜面ですから ２ 〔ｍ〕と、真上に引き上げる距離の２倍になります。 よって、Ｂくんのする仕事は、  と、Ａくんと同じ仕事となります。 このように
これを「仕事の原理」といいます。 |
||||
| 教科書ｐ92 問39（改） 水平となす角が 30°のなめらかな斜面上で、質量 10ｋｇの物体を、斜面に沿ってゆっくりと 4.0ｍ引き上げた。重力加速度の大きさを 9.8ｍ/ｓ２として以下の問いに答えよ。 (1) 加えた力の大きさは何Ｎか。 (2) この力がした仕事は何Ｊか。 ＜解答＞ (1) 斜面が水平となす角が 30°だから、物体にはたらく重力の、斜面に平行な分力の大きさは、  よって、物体に加えた力の大きさは、49 Ｎ (2) この力がした仕事は、 ＝＝49×4.0＝196 答え 2.0×10２ Ｊ＜参考＞ 上の問題で、質量 10ｋｇの物体を、斜面を用いずに同じ高さまで引き上げる仕事を求めます。 上の問題のように 30°の斜面にそって 4.0ｍ引き上げる場合、高さ 2.0ｍまで引き上げることになります。 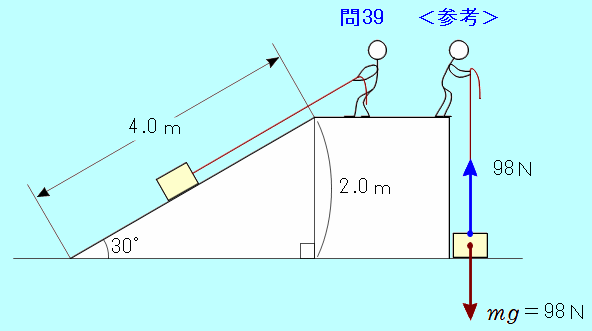 真上に物体を引き上げるのに必要な力は、荷物にはたらく重力と等しく、 ＝10×9.8＝98Ｎよって、物体を高さ 2.0ｍまで引き上げる仕事は、 ＝＝98×2.0＝196 よって 2.0×10２ Ｊ 上の問39と同じ仕事の量になり、「仕事の原理」が成立していることがわかります。 |
||||
| → 動滑車の例 へ |
||||
| |
||||
| |
||||