 浮力の式の別の導き方(教科書p83上部「浮力の式を導こう」) 浮力の式の別の導き方(教科書p83上部「浮力の式を導こう」)
図のように、水中にある直方体の物体を考えます。物体は、四方八方から水圧による力を受けています。
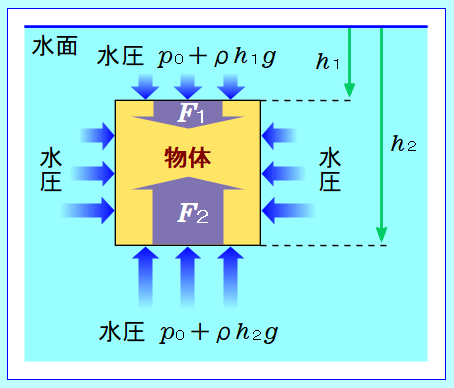
 側面が受ける力は、左右、前後でつりあっているので、考えなくていいこととします。 側面が受ける力は、左右、前後でつりあっているので、考えなくていいこととします。
 上面が受ける力と下面が受ける力は、水圧のところで学んだように、水深が深くなるほど水圧が大きくなるので、 上面が受ける力と下面が受ける力は、水圧のところで学んだように、水深が深くなるほど水圧が大きくなるので、
(下面が受ける力)>(上面が受ける力)
となります。
 この力の差、(下面が受ける力)−(上面が受ける力)=浮力 この力の差、(下面が受ける力)−(上面が受ける力)=浮力
となるのです。
(復習)
・ 面積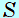 に力 に力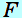 がはたらき、圧力 がはたらき、圧力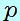 とすると、 とすると、
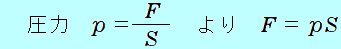
・ 深さ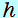 の地点の水圧 の地点の水圧 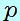 = = 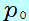 + +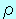 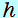 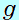
|
 上図の文字を用いて式を書くと、 上図の文字を用いて式を書くと、
 面積 面積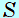 の上面が受ける力 の上面が受ける力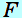 1 1
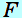 1= 1=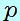 1 1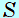 =( =(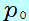 + +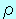 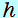 1 1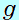 ) )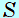 (小さい) (小さい)
 下面が受ける力 下面が受ける力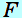 2 2
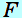 2= 2=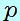 2 2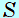 =( =(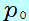 + +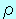 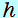 2 2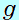 ) )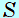 (大きい) (大きい)
 浮力 浮力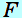 = =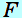 2− 2−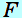 1 1
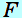 = =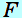 2− 2−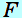 1=( 1=(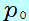 + +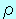 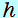 2 2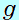 ) )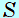 −( −(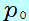 + +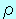 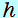 1 1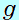 ) )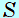
=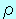 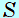 ( (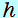 2− 2−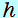 1) 1)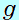
ここで、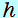 2− 2−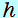 1 は物体の高さですから、 1 は物体の高さですから、
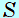 ( (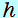 2− 2−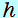 1)= 1)=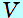
物体の体積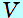 となります。 となります。
よって、
浮力の式が導かれました。
 教科書p83 問34 教科書p83 問34
密度 7.0×102kg/m3、体積 2.0×10−3m3の木片全体を水に沈める。水の密度を 1.0×103kg/m3、重力加速度の大きさを 9.8m/s2とすると、木片が受ける浮力の大きさは何Nか。
|
