等加速度直線運動の3本の式(8) |
|
<チャレンジ問題> 高速道路を北に向かって 20m/sで走行する自動車が、ブレーキをかけてから 50m進んで止まった。その間、自動車は等加速度直線運動をしたものとする。 <状況> 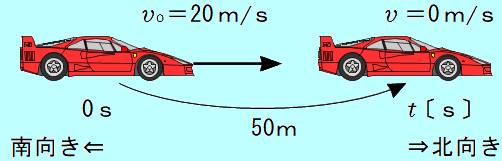 北向きを正の向きとして考える (1) 自動車の加速度を求めよ。 速度が 0m/sとなるまでの変位 50m( 02−202= 2× −400 = 100 答え 南向きに 4.0 m/s2 (2) 自動車がブレーキをかけてから止まるまでの時間を求めよ。 式では、加速度 0 = 20 +(−4.0)× 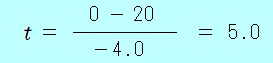 答え 5.0 秒 <別解> ただし、2本目の式は 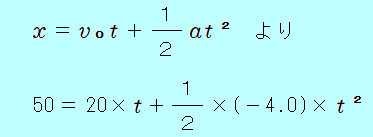 50 = 20 25 = 10 この2次方程式を解きます ( よって、 答え 5.0 秒 やっぱり、1本目の式を使ったほうが簡単ですね。 等加速度直線運動の3本の式、簡単でしょ? 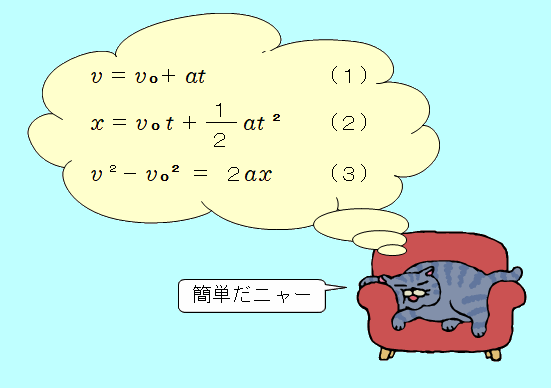 | ||
| → 初めにもどる |
||
| | ||