速度の合成

速度の合成（７）

（平面上の速度の合成）
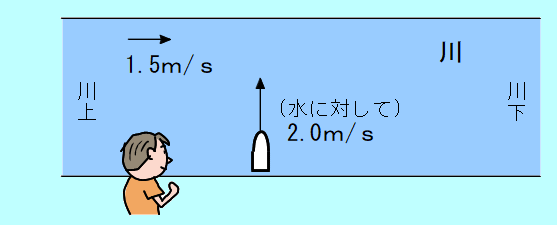
　今度は、船が、船首を岸と垂直に、対岸に向けて川を横切って進む場合を考えます。

（教科書ｐ20 問９）
　静水の場合に速さ 2.0 ｍ/ｓで進む船が、流れの速さ 1.5 ｍ/ｓの川を、船首を流れに直角に向けて渡る。このとき、岸で静止する人から見た船の速さは何ｍ/ｓか。

ベクトルの和で合成速度を求める方法
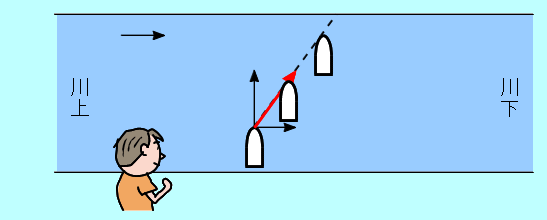
　正負で向きを表すことができませんので、ベクトルの和で合成速度を求めます。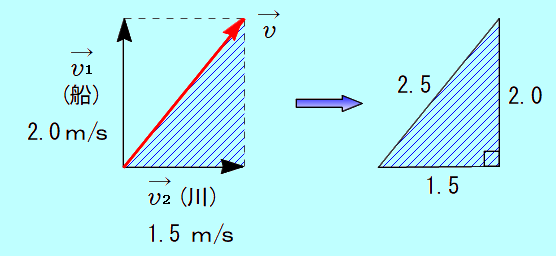

　平行四辺形の法則で

を求めます。

　上の合成の図より、三平方の定理を使って、

　　　　

＝ 2.5 ｍ/ｓ　となります。

　よって、　岸で静止する人が見た船の速さは 2.5 ｍ/ｓ　です。

　下図のようなイメージです。船は、毎秒 2.0ｍずつ対岸に近づき、毎秒 1.5ｍずつ下流に流されることになります。

＜ヒント＞
物理でよく出てくる直角三角形　

30°、60°、90°の直角三角形　　辺の比は、１：２：

45°、45°、90°の直角三角形　　辺の比は、1：1：

辺の比が、３：４：５の三角形　　（三平方の定理　３^２＋４^２＝５^２となるから）　

辺の比が、12：13：５の三角形　　（三平方の定理　12^２＋５^２＝13^２となるから）　

上の問題では、３：４：５の直角三角形になることに気がつけば、三平方の定理を用いなくても、簡単に

＝2.5 m/ｓと答えることができます。

　→ 初めに戻る　

　

　

　