位置エネルギー（４） |
   |
位置エネルギー（４） |
|
 弾性力による位置エネルギー（教科書ｐ98）伸ばされたばねにつながれた物体は、ばねが自然の長さに戻るとき、ある速さとなり、運動エネルギーを持つことになります。したがって、伸ばされたばねにつながれた物体は、仕事をする能力（エネルギー）を持つことになります。縮められたばねにつながれた物体についても同様です。 このような、伸ばされた（縮められた）ばねにつながれた物体が持つエネルギーを、「弾性力による位置エネルギー」といいます。
＜補足＞ 「弾性力による位置エネルギー」は、伸ばされた（縮められた）ばねにつながれた物体がエネルギーを持つという考え方です。伸ばされた（縮められた）ばねそのものがエネルギーを持つという考え方もあり、その場合は、ばねの「弾性エネルギー」と使い分ける場合があります。どちらの考え方でもかまいません。
伸ばされたばねにつながれた物体が、ばねが自然の長さに戻ったときにどれだけの運動エネルギーを持つのかを求めます。自然の長さから  〔ｍ〕伸ばされた、ばね定数 〔Ｎ/ｍ〕のばねが自然の長さに戻るまでに、物体にどれだけの仕事をするのかを考えます。物体についてのエネルギーの原理（運動エネルギー変化＝された仕事）から、ばねが自然の長さに戻ったときに物体が持つ運動エネルギーがわかります。 つまりそれが、はじめに物体が持っていた弾性力による位置エネルギーとなります。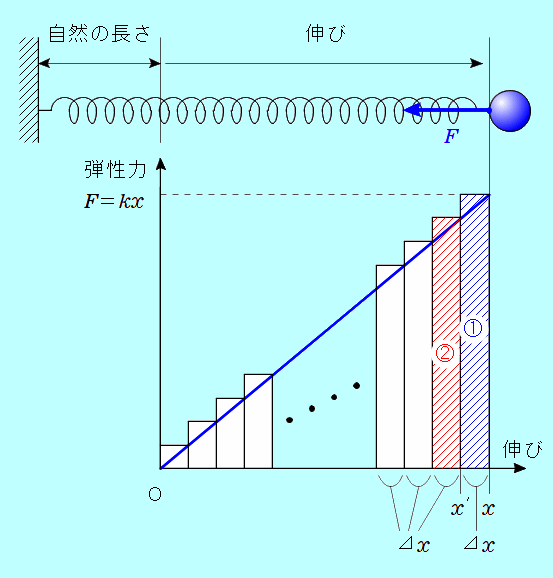  
上のグラフの青い直線は、ばねの伸び と ばねの弾性力 の関係を表します。ばねの伸びが のとき、ばねが物体を引く力は  ＝です。この力で、ばねは、図の  まで、わずかな距離 （デルタ：わずかな距離）だけ引くとします。この間にばねがする仕事は、 ×で、図の斜線をつけたの長方形の面積で表されます。 ばねの伸びが となったあと、弾性力 の力で、さらにだけ引くとします。この間にばねがする仕事は、図の斜線をつけた 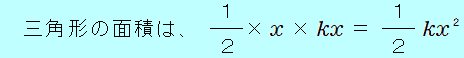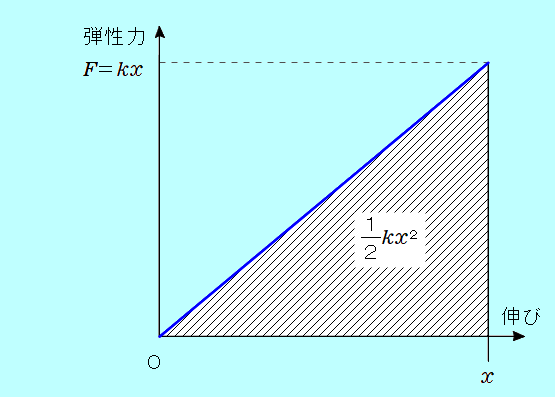の長方形の面積で表されます。 以下同様に、ばねが自然の長さに戻るまで、ばねがする仕事を少しずつ分解して考え、（わずかな距離）をすごく細かくしたとすると、その合計は、下の図の、斜線をつけた三角形の面積で表されることがわかります。  よって、ばねが自然の長さに戻るまでに、物体はばねから 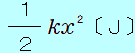 の仕事をされることになります。
|
|||||
| → 練習問題 へ |
|||||
| |
|||||
| |
|||||
で表します）は、