 仕事(教科書p88) 仕事(教科書p88)
「仕事がはかどった」とか「どんな仕事してるの?」とか、いろんな場面で「仕事」という言葉を使いますが、物理でいう「仕事」は、次の意味で用います。
物体に力がはたらき、力の向きに物体が移動したとき、
その力が「仕事をした」といいます。 |
 例1 例1
図のように、物体に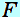 〔N〕の大きさの力を加え、距離 〔N〕の大きさの力を加え、距離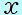 〔m〕移動させた場合 〔m〕移動させた場合
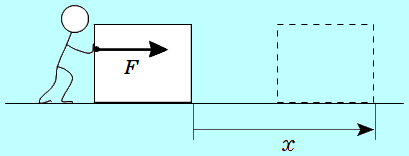
この力が物体にした仕事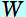 は力の大きさ は力の大きさ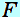 と移動距離 と移動距離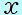 の積で次のように定められます。 の積で次のように定められます。
「仕事」は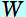 (workの頭文字)で表します。 (workの頭文字)で表します。
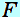 の単位にN(ニュートン)、 の単位にN(ニュートン)、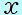 の単位にm(メートル)を用いるとき、仕事 の単位にm(メートル)を用いるとき、仕事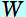 の単位にはJ(ジュール)を用います。 の単位にはJ(ジュール)を用います。
人の名前が元になる単位ですので、大文字で表します。
 例2 例2
図のように、斜め上に引く場合
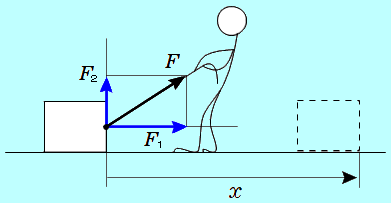
力の向きの斜め上に、荷物は持ち上がってきません!
斜めの力を、荷物が移動する方向と、それに垂直な方向に分解します。
荷物が移動する方向の分力を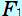 、垂直な方向の分力を 、垂直な方向の分力を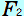 とします。 とします。
 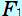 の向き(横向き)に荷物が の向き(横向き)に荷物が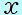 だけ移動するので、この場合の仕事は だけ移動するので、この場合の仕事は
と表すことができます。
なお、
 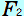 の向き(上向き)に荷物は移動していませんので、 の向き(上向き)に荷物は移動していませんので、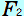 のする仕事は 0Jです。 のする仕事は 0Jです。
三角関数を使う場合
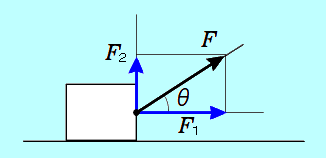
力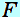 を分解するときの直角三角形に着目して、 を分解するときの直角三角形に着目して、
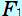 = =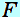 cos cos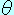
と表すことができます。
よって、
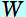 = =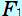 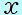 =( =(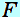 cos cos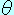 )× )×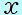 = =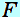 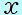 cos cos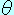
斜めに引く場合の仕事は
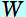 = =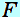 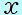 cos cos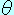 ……教科書p89(60)式 ……教科書p89(60)式
|
 例3 例3
図のように、人力車が加速しないように坂道を下る場合。
(力の向きと移動の向きが逆向きの場合)

これは危険です。
油断すると人力車がどんどん加速して、引いていた人が人力車にひかれて、マンガのようにヒラヒラヒラとなってしまいます。

そこで、加速しないように、後ろに力を加えながら、前に進んでいきます。
力の向きと移動の向きが逆向きの場合の仕事は、
と表します。
上の、力の向きと移動の向きが逆向きの場合について、
斜めに引く場合の仕事の式
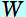 = =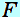 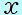 cos cos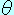
で考えると、力の向きと移動の向きが逆向きの場合は
cos180°=−1
ですので、
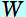 =− =−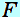 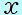
となります。
90°<θ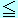 180°の場合、 180°の場合、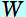 <0(負の仕事)となります。 <0(負の仕事)となります。
|
|



