動摩擦力（３） |
   |
動摩擦力（３） |
|
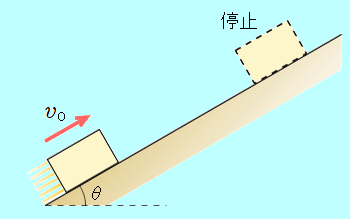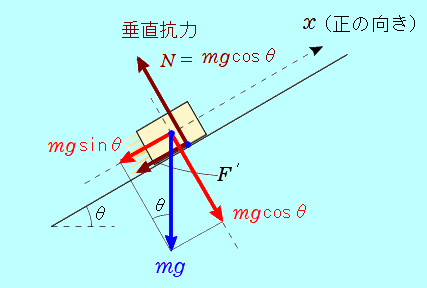 ここでは斜面上における動摩擦力を学びます。 教科書ｐ78 類題13水平となす角が  の粗い斜面上で、質量 〔ｋｇ〕の物体に初速 〔ｍ/ｓ〕を与え、斜面に沿って上向きにすべらせると、しばらくして停止した。この間の物体の加速度を求めよ。また、斜面上をすべった距離は何ｍか。ただし、物体と斜面との間の動摩擦係数を 、重力加速度の大きさを 〔ｍ/ｓ２〕とする。 解答 図のように、重力を斜面に平行な方向、斜面に垂直な方向に分解すると、 斜面に平行な分力の大きさは  sin斜面に垂直な分力の大きさは cos物体が斜面から受ける垂直抗力の大きさは  ＝cos物体が斜面から受ける動摩擦力の大きさは  ＝ ＝ cosここで、初速度の向き（斜面に沿って上向き）を正の向きとして物体の運動方程式を書くと  より ＝− sin− cos＝− sin− cos＝− （sin− cos）よって、加速度は 斜面に沿って下向きに （sin− cos） 〔ｍ/ｓ２〕 停止するまでに斜面上をすべった距離等加速度３番目の式 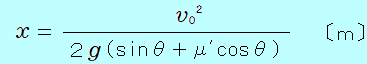 ２−２＝２ より０２− ２＝２×｛−（sin− cos）｝×よって  上の「類題13」では、斜面に沿って上向きにすべるので、動摩擦力は斜面に沿って下向きとなります。教科書の一つ前の「例題13」では、物体が斜面に沿って下向きにすべるので、動摩擦力は斜面に沿って上向きになります。 動摩擦力は、運動を妨げる向きにはたらくので、運動の向きと常に逆向きになります。  |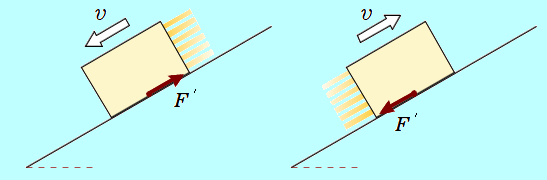
||
| → 動摩擦力（＋等加速度運動）の確認問題 へ |
||
| |
||
| |
||